В комментах к прошлому посту выяснилось, что не все знают, как СССР испортил преподавание математики в школах в 1970–1978 годах.
Самые худшие злодеяния совершаются, как известно, из самых лучших побуждений.
Группа инициативных советских математиков под руководством Колмогорова решила изменить как преподаётся математика в средних школах. Мол, мы живём во время науки и техники, а детей учим по дореволюционному учебнику Киселёва (что было сущей правдой — и мою бабушку, и моего отца учили именно по Киселёву).
Основная претензия маститых академиков к Киселёву состояла в том, что в его учебниках есть «неточности», «допущения», и что учебник «не является строго математически точным». Что формально тоже правда. НО! Почему там были «неточности» и «допущения»? Что, кандидат наук Киселёв не знал математику? Разумеется, знал! Но главное отличие Киселёва от маститых академиков было в том, что в отличие от них, Андрей Петрович 20 с лихером лет преподавал математику в гимназиях и училищах. И именно потому, что он был Учителем, он знал, как именно нужно давать математику детям разных возрастов. Ведь ум ребёнка постоянно развивается — и вместе с ним его способности к пространственному воображению, абстрактному мышлению, и так далее. Если мы начнём фигачить в пятиклассника преподаванием на уровне университета, он ничему не научится.
Но академики пробили свою инициативу и решили, что им лучше видно, и начали писать свои учебники и портить киселёвские (особенно отличился на этом поприще некий Глаголев). В результате в учебниках математики и геометрии для средней советской школы появились абсолютно точные математически определения, доказательства и теоремы… абсолютно непонятные школьнику, ибо заумь.
Не буду голословным.
Все знают, что такое равные треугольники?
Вот доказательства того, что треугольники равны, если у них две одинаковые стороны, и одинаков угол между ними. Сначала — учебник 1980х Погорелова (по которому учили меня), а потом — Киселёв.
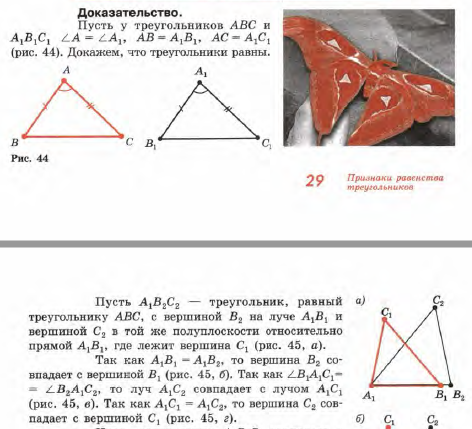
Ну чо, всё поняли? Я до сих пор нихера не понимаю. Луч, полуплоскость какая-то, и что меня добивает — иллюстрация якобы равных треугольников, явно не совпадающих друг с другом.
А теперь — умница наш Андрей Петрович Киселёв:
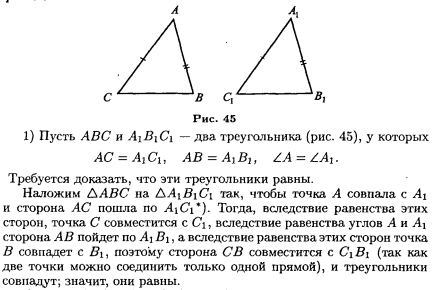
Вот тут всё предельно понятно, не так ли? Треугольники наложились и совпали? Конечно. И всё сразу ясно.
Но академики взъелись — чо тут? Какая это «точка»? Её правильно называть «вершиной!» И так далее и пошло-поехало. А то, что теперь эту заумь даже взрослый мужик не понимает — ну, не наши проблемы. В наших доказательствах и теоремах зато всё точно!!
И каков же был результат? Результат был АХОВЫЙ. В 1980х годах, казалось бы, в «золотые годы» советского образования стандартные задачки из дореволюционного задачника по математике решало вдвое меньше учеников. Я уж не говорю о гимназических контрольных — их вообще могли решать только школьники математических спецшкол.
Пример задачки для пятого класса: В классе 28 человек. Отношение числа девочек к числу мальчиков равно 4⁄3. Сколько в классе девочек?
В 1950м году её решило 83% пятиклассников. В 1995 — 37%!! То-есть, это вообще регресс, причём регресс абсолютный!
Спасибо вам, маститые академики, вы добились чего хотели — стало хуже. А советские школьные учебники теперь я вспоминаю исключительно матом.
Я бы хотел тут добавить «а зато в Америке.…» но, увы, не могу. Американское школьное преподавание математики разломали ещё в 1960х (из тех же благих побуждений, ёпрст — они решили, что математику надо преподавать «лучше», так как СССР обгонял США в космической гонке). А недавние инициативы «No Child Left Behind» и «Common Core» опустили планку обучения вообще ниже плинтуса. У меня и свояченица и тёща учители. О новомодных введениях, которые запустили ещё при Буше-младшем они говорят исключительно нецензурными словами.