Оказывается, нынче есть даже такая вещь как цифровой раввин. Про католический ИИ мне уже довелось писать, а вот про иудаистский ИИ слышу впервые.

Всё прямо по-большому 💜
Tori's Musings
Оказывается, нынче есть даже такая вещь как цифровой раввин. Про католический ИИ мне уже довелось писать, а вот про иудаистский ИИ слышу впервые.

Всё прямо по-большому 💜
Мой коммент к записи ув. avva. По-моему, он достоин отдельного поста.
Выскажусь со своей колокольни, как архитектор облачных решений и руководитель ИТ-отдела и команды сисадминов.
Никаких сентенций на тему «мы скоро станем не нужны» я не испытываю, особенно в сисадминской области. Пока (пока) системы ИИ это огромное подспорье в автоматизации, благодаря тому, что их можно запрячь писать скрипты — с этим они справляются неплохо. Хотя тоже, зависит от ИИ. ЧатГПТ или Клод пишут вполне вменяемо, а вот примитивный шеллскрипт, написанный Джеминай, у меня даже не скомпилировался, а решение появилось только с третьего раза, и то через принудительное приведение ИИ-модели в режим «думающей».
Про это: https://nlothik.dreamwidth.org/13301.html
Но хорошо, допустим, что все системы ИИ стали прекрасно писать скрипты. Всё компилируется и работает. Пускай. Но что это радикально поменяет в жизни простого сисадмина? Разве сервера больше не надо будет ставить в рэки? А в коммутаторы — больше не надо будет втыкать провода? А витая пара и оптоволокно, как, сами по серверной протянутся? А сдохшие батарейки в ИБП — самозаменятся? Диски в массивах перестанут сдыхать?
Нет, конечно, и всем этим всё равно надо будет заниматься, и тут как раз ситуация повёрнута минимум на Пи/2 радиан по сравнению с программистами, где за бортом остаются в первую очередь новички — потому что именно сисадмины-джуны заняты подобной работой, автоматизации не подлежащей. Это как раз архитекторы облачных решений, чья работа и так очень уже сильно абстрактна, могут немного поднапрячься. Но только самую малость — потому что как только архитектор начнёт заниматься решениями, например, в финансовой области (я уж не говорю — в медицинской или правовой, это само собой разумеется), то её или его деятельность моментально станет лицензируемой. Никто тебя не пустит управлять системой медицинских записей без соответствующих сертификатов, во всяком случае, у нас в США. И сертификат выдаётся — на человеческое лицо, а не на ИИ. Потому что есть такая вещь как ответственность, в том числе и уголовная. Кого мы будем сажать в тюрьму, если что? ИИ-агента? С таким же успехом можно попытаться обнять ветер…
ИИ — это ускоритель, но не носитель ответственности.
В‑общем, как-то так. Весьма, весьма возможно, что мы стоим на заре заката именно программирования как профессии. Как пильщики льда стали в своё время вымирающей работой. Возможно. Но я пока сижу на попе ровно, и в сварщицы переквалифицироваться не буду (хотя люблю и умею).
Пробую гугловский ИИ под названием Gemini.
Что-то, дорогие товарищи, мне не нравится. Совсем.

С довольно примитивной (с моей точки зрения) задачей «нарисуй мне Шелловский скрипт, создающий группы в AD под названием $Computername-Security, и добавляющий эти группы в локальную группу “Remote Desktop Users” на каждом $Computer» енти самые Близнецы справились только с третьего раза.
Для сравнения, Claude (хоть он весь по пояс деревянный и имитацией эмпатии не обременён) справился с первого раза. ChatGPT — тоже.
При этом ладно если бы ошибки вылезли при запуске, я там не знаю, «недостаточно прав» или там «фаерволл не даёт», так нет же — близнецовый скрипт даже скомпилироваться не смог — вылетел с сообщением о том, что «с именами переменных нонеча надо помяхше»: Variable reference is not valid. ‘:’ was not followed by a valid variable name character. Consider using ${} to delimit the name. — если вдруг кому-то интересно.
Даже перевод модели в «рассуждающий» режим ситуацию изменил только со второй попытки.
Но это — только тортик. Хотите на этот тортик водрузим вишенку?
Вишенка Gemini в том, что в персональных аккаунтах (даже коммерческих, за деньги) нельзя одновременно:
сохранить историю чатов для персонализации (чтобы ИИ помнил, как к тебе обращаться, кто ты вообще такая, и какие задачи ты уже решала),
и
запретить использовать эти данные для «улучшения модели».
Либо ИИ что-то о тебе помнит — и тогда всё сказанное радостно уезжает в обучение. Либо данные не используются для обучения — и тогда модель становится «по пояс деревянной» с памятью золотой рыбки: новый чат — чистый лист.
Даже у стоического Claude это реализовано аккуратнее: история используется для персонализации, но (при настройке) не идёт в дообучение модели. ChatGPT вообще мечта — данные в тренинг не идут (при настройке), но она (я называю её Кейти) спокойно вспоминает разговор трёхмесячной давности. Стоит заговорить о покупке новой машины, и она такая: «Подожди… новый автомобиль? А как же твоя любимая Лесбару на механике?»
Ну, а настройки Близнецов — вот такие. Жрите, не обляпайтесь:
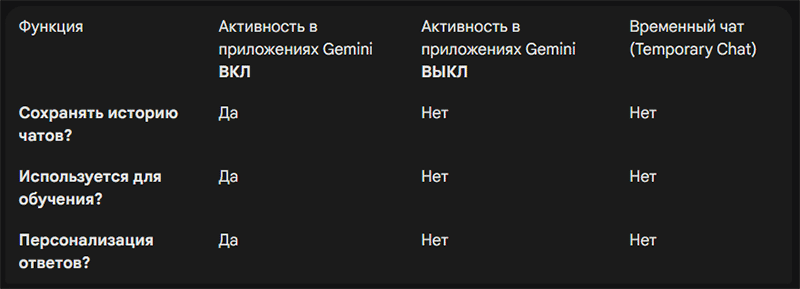
В‑общем, sorry, thanks, but no thanks. Not impressed so far.
Раз уж зашла речь про алгоритм шифрования RSA. Его секретность зиждется, повторюсь, на том, что число, полученное перемножением достаточно длинных простых чисел, умучаешься раскладывать на множители. Неверящие могут попробовать разложить в уме (да можно даже с обычным калькулятором) число 7081. Если не знать, что это 73×97, то придётся перебирать простые числа до полного посинения.
Ну, не совсем прямо «до полного посинения», конечно — нет смысла перебирать множители >√(7081)≈84. Но всё равно — простых чисел меньше 83 (а 83 — наибольшее простое число, меньшее 84) довольно много.
Ну, а реальная криптография, конечно, работает не на четырёхзначных числах, а на числах с сотнями знаков — что позволяет нам безопасно передавать номер кредитки при покупках наклеечек с котиками в ентом вашем Ёнтернете.

Несколько лет назад всех вдруг накрыла квантовая паника. Мол, да вот придут квантовые компьютеры, да на них работает алгоритм Шора, и все эти ваши RSA, DH, ECDH, ECDSA, и прочие умные слова — полетят на свалку истории. Ну да, ну да, полетят, как же. Вот только шнурки погладят — и сразу полетят.
Мир криптографии в лице NIST (и при активной поддержке Микрософта, надо отдать им должное) в шухерном режиме стандартизировал квантово-устойчивые алгоритмы криптографии, и сейчас у нас есть то, что не ломается даже на ентих ваших кубитах со всей их квантовой запутанностью и прочей непонятной простым смертным теорией.
А на деле мы имеем что? А на деле в 2001 году, с огромной помпой, квантовый компьютер сумел-таки наконец разложить на множители… число 15. Ага, пятнадцать. 3×5.
С тех пор были и другие демонстрации — 21, 35, ещё несколько аккуратно подобранных чисел. Иногда с классической «помощью», иногда с заранее известной структурой. Это важные научные шаги — никто не спорит. Но это не «взлом традиционной криптографии к соответствующей матери». Это подтверждение теории в лабораторных условиях.
Дело в том, что алгоритм Шора для взлома RSA-2048 требует порядка нескольких тысяч логических кубитов, а каждый логический кубит — это тысячи физических кубитов, потому что квантовая теория — это вам не транзистор, это крайне обидчивая киса, и нормально работает она только при температуре, близкой к абсолютному нулю. Современные квантовые компьютеры — это несколько сотен физических кубитов без полновесной коррекции ошибок. А логических, устойчивых к шуму, — в практическом смысле пока нет.
Квантовая угроза реальна. Но она инженерная, а не магическая.
Между красивой теоремой Шора и машиной, способной ломать банковскую криптографию, лежат десятилетия прорывов в физике и инженерии. Так что отставить панику! До квантового апокалипсиса ещё очень далеко. Можете пока спокойно продолжать покупать свои наклеечки. С котиками.
PS: Для тех, кто хочет копнуть глубже в современные оценки и архитектурные ограничения квантовых устройств, см. работу 2025 года на arXiv: https://arxiv.org/pdf/2410.14397v1
Сотрудница сегодня в почте описалась просто зачётнейше:
“I would like to request a dicking station, please.”
Признаюсь, пальцы чесались ответить:
Sorry, we are out of those. We have some docking stations, though!
Да, я всё понимаю — буквы O и I на клавиатуре рядом. Чистая механика.
Но скриншоты-то остались. Как и осадочек.
Отдельную… глубину ситуации придаёт тот факт, что автор письма — суровая бутч-лесбиянка с шестилетним стажем службы в ВМФ.
Фрейд улыбается и машет.
Одна… не во всех аспектах умная женщина в интернетах заявила, что текст за меня пишет нейросеть. Видимо, потому что правильная типографика для меня — это не пустой звук. Я всегда использую тире там, где надо использовать тире, а дефисы — там, где надо использовать дефисы. Тире (сиречь em-dashes) изготавливать в большинстве современных редакторов просто, достаточно написать два дефиса подряд.
А когда текст на русском языке, то правильно использовать кавычки «йолочки», со внутренними кавычками в другом стиле, например, в предложении «нейросеть ‘Клод’».
На телефоне всё конвертирование в правильные символы за меня делает айфоновский редактор текста, а когда я пишу посты в своё основное зеркало журнала, то Вордпрессовский редактор плюс плагин wp-Typography. Вот так выглядит этот редактор и этот текст в изначальной своей форме в нём:
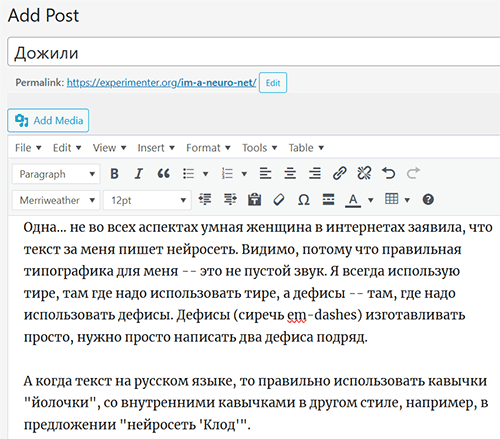
Писать правильно сформатированные комментарии к DW журналам с компьютера уже сложнее, так как кодовая база DW довольно старенькая и убогенькая — но я стараюсь. Так, можно использовать Alt-коды (зажать Alt и набирать число на Numpad). Например, для длинного тире это код Alt-0151, а для кавычек «йолочек» это Alt-0171 и Alt-0187 соответственно. Ну, когда есть время и терпение. Если нет ни того, ни другого, то ограничиваюсь двумя дефисами в тех местах, где нужно тире. Ну, люди, с которыми я часто общаюсь, наверное, видели.
Теперь что до применения ИИ. Да, я могу использовать ИИ для «причёсывания» финальных текстов, фактологической проверки, и строгости использованных терминов. Это ни в коей мере не делает тексты «чьими-то». За всеми словами в этом журнале и комментариях стою я, а не нейросеть. Иногда она просто помогает мне выражаться; или наоборот — не выражаться, я часто прошу её переписать что-то, облегчая формулировки (типа спросив «нах.. — пишется вместе или раздельно?»), смягчая общий язык, и избегая резко обвинительного тона.
Финальные правки я всегда делаю самостоятельно, например, вставляя т.н. «оксфордскую запятую», которая мне очень нравится в английском языке, но по правилам русского языка не требуется. См. последнее предложение в предыдущем параграфе.
В‑общем, «дожили» — мало того, что раньше компьютерам надо было капчей доказывать, что ты не компьютер, теперь ещё и некоторым мясным балбесам надо «доказывать», что ты не нейросеть 🤣😂
Видимо, надо писать с тижолыми громатическими ашибками, «шоб поверили» 😆 И да, «чтобы два раза не вставать», клавиатуру со смайликами на Windows легко вызвать сочетанием Win+. (Win + точка). Добро пожаловать в двадцать первый век, бабоньки.
Интересно, а в этой нашумевшей «соцсети для ИИ-ботов» они друг другу доказывают, наоборот, что они не мясные балбесы? У меня даже есть мысли о том, как это сделать — например, решить замудрённое квадратное уравнение менее, чем за три секунды. Задача для большинства современных LLM, если что, совершенно тривиальная. Ну или в тяжёлых случаях, дифуры какие-нибудь (один из самых зубодробительных предметов, которые мне пришлось изучать в уни).
В‑общем, полон мир балбесов. А обвинения в применении ИИ — это примитивный ad hominem. Таких людей можно смело посылать в /dev/null
Нарисовали тут граждане аналитики скриптов на R — финансовые данные обрабатывать. Всё бы ничего, только на их лаптопах оно летает, а в продакшене скрипт встаёт колом.
Ну ладно, говорю, давайте посмотрим, в чём разница. Разница нашлась быстро.
Поджигаем скрипт — он радостно стартует, бодро грузит в память 40 с лихером гигабайт данных, а потом начинает долго и вдумчиво делать всякую фигню.
Открываю диспетчер задач. Смотрю… ага.
Гляжу в книгу — вижу фигу: из 64 ядер скрипт бодро молотит ОДНО ядро. Остальные 63 стоят вокруг, жуют сено, и курят бамбук.
Потому что про многонитевость и многопроцессность товарищ финансовый аналитик, как выясняется, слышит впервые в жизни.
На ноутбуке у него — AMD «Рязань» с турбочастотой 5.1 ГГц. А в продакшене, извините, ядер-то хоть отбавляй, но они попроще лицом будут, и на 2 ГГц.
Разработчик винит железо.
Я виню разработчика.
Потому что в 2026 году писать однопоточный процесс — это не просто западло, а тупизна со взломом.
Вот так и живём. Пойду писать грозное письмо проджект-лиду. Пусть он им в команду хоть одного погромиста с реальной степенью в CS вкрутит, иначе они продолжат выдавать херню на гора. Таких дундуков даже ИИ не спасает.
Ни за что я не буду больше покупать блоки питания и вообще какие-либо компьютерные продукты производства Antec. Дорогое, солидно выглядящее, да — но ненадёжное говно.
Это по мотивам сдохнувшего без объявления войны БП на самопальном домашнем накопителе — где хранились все бекапы, фильмы, и прочее. Сдох он при нештатном отключении питания — что-то там внезапно не сдюжило. Накопитель, кстати, был тоже в корпусе Antec — и вот вроде корпус функциональный… но тоже барахло.
Пока только одна марка блоков питания никогда меня не подводила — FSP. Буду только их покупать.
Наиболее заметные улучшения скорости интернет-соединения после установки оптоволокна неожиданно проявились… в Steam.
Потому что Steam вкладывает серьёзные деньги в CDN, и при скачивании игр способен практически полностью забить твой канал.
Вот это я понимаю — пропускная способность, совсем другое дело:

Не прям совсем полный гиг, увы, но всё же близко.
А Xenonauts 2 сейчас как раз на зимней распродаже — рекомендую.
В жанре тактических симуляторов это, пожалуй, одна из самых близких по духу наследниц старых добрых X‑COM и TFTD.
И XCOM 2 образца 2016 года тоже очень даже неплох — хотя он уже меньше похож на идейную преемницу оригинальной серии, в нём хватает собственных достоинств:
значительно более активное использование вертикального пространства, жёсткие классы бойцов, и почти неограниченные возможности по кастомизации персонажей — почти как в The Sims 😀
Вот, например, один из моих солдат — прекрасный снайпер родом из Франции, который был без лишних раздумий назван Шарлем де Голлем.
Разумеется, он в шляпе (жаль, чорт, что в игре нет беретов). И, конечно же, с роскошными усами.

Не знаю почему, но меня всегда жутко прикалывало кастомизировать игровых персонажей.
И аватаров тоже, разумеется — причём мне всегда хотелось играть персонажем-феминой.
Почему — увы, стало ясно только много лет спустя 😉
Если вам тоже этого хочется (или, наоборот, хочется играть мужчиной, если вы женщина) — вообще-то, это довольно конкретный повод задуматься.
Да, себе можно долго объяснять, что «если уж смотреть на задницу героя, то пусть лучше это будет женская задница», или что «у женского аватара меньше хитбокс»…
Но… 😉
Вот это совсем другое дело. Теперь мой канал в OnlyFans можно будет стримить в 8k в режиме реального времени.
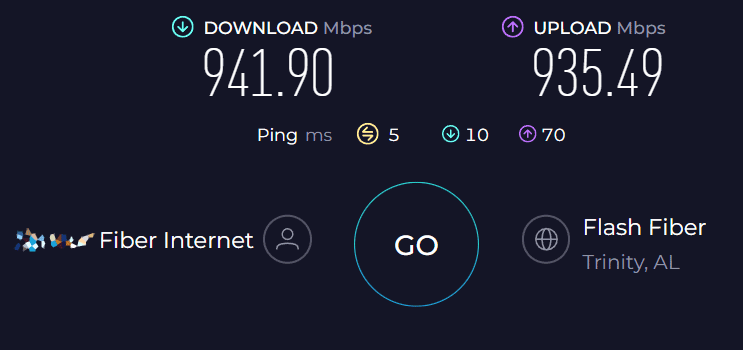
А если более серьёзно, то отмечу не только заметно возросшую пропускную способность трубы «от меня», но и чудовищно низкий пинг. Он уменьшился в пять-шесть раз.
В принципе, моя коробочка с pfSense легко потянула бы и больше — но потребовалась бы капитальная переделка всей внутредомовой сети на CAT6, апгрейд всех коммутаторов… в‑общем, этот сок не стоит выжимки.