Category: учёба

Как говорится, hot take.

Правильно сделал товарищ Доня Козырев сотоварищи. Гнать их под жопу коленом, сели только на шею, а выхлоп нулевой. Чем они вообще занимаются? Ну вот давайте почитаем.

Ну вот возьмём перечисление обязанностей с USA Facts:

Департамент образования (Education Department, ED) — это исполнительное ведомство на уровне кабинета министров, отвечающее за надзор за политикой в ​​области образования и управление финансированием программ и отдельных лиц. Функции департамента включают поддержку государственных и местных систем образования, содействие равенству в образовании для всех студентов и предоставление грантов и кредитов высшим учебным заведениям и студентам.

По всем позициям — полный провал. Политика образования в Соединённых Штатах, во всяком случае на уровне среднего образования — абсолютно кретинская. Поговорите с любым американским учителем — узнаете много нового. У меня свояченица преподаватель математики в школе. Про федеральные инициативы типа https://en.wikipedia.org/wiki/No_Child_Left_Behind_Act и https://en.wikipedia.org/wiki/Every_Student_Succeeds_Act выражается исключительно нецензурной бранью. Кстати, о математике. Способы преподавания математики, начатые Common Core — абсолютно идиотские. В 2013 году наш штат, слава Аполлону, из этой бредятины вышел, но математику всё равно продолжают преподавать как Common Core. То-есть, по-идиотски — зубрением методов получения ответа, а не получению правильного ответа на вопрос. Они думают, что умение ответить на вопрос “сколько будет дважды два” шестью разными способами (я практически не преувеличиваю) что-то сдвинет в уме второклассников, и сподвигнет их на более глубокое понимание математики. Неа, не сдвинет. Они просто запутаются. Метод получения ответа должен быть, особенно на начальном этапе, только один. Все вот эти инициативы по сложению двух чисел разбиением на всё более мелкие и мелкие части — в два раза длиннее, и учит методу, а не получению правильного результата. Складывать большие числа надо в столбик.

Скриншот из видео, объясняющего методы Common Core, в частности один из способов сложения чисел Common Core Math. Слева — сложение в столбик, как нормально учили нас, наших пап и мам, и бабушек с дедушками. Справа — современная ересь.

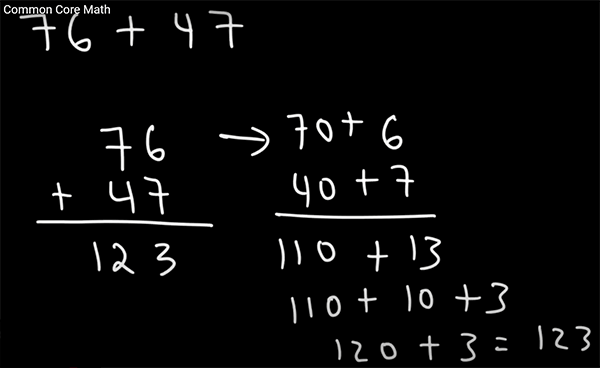
“Да, так тоже можно”, но на кой чорт? Вот мы с вами или наши бабушки, что, не сможем сложить два числа, что ли? Клянусь Юноной, мы как минимум получим ответ быстрее! Да, и если хотите окончательно охренеть, поглядите там, как они предлагают большие числа умножать — один метод, это, напроимер, раскладывание умножаемых чисел на суммы в скобках, их раскрыванием, и т.д. Поседеть можно к тому моменту, когда ответ получишь.

Гнать в шею того, кто всё это придумал и внедрил. И добавить коленом под жопу.

Ну да, тут можно возразить — “а если твой штат вышел из этой национальной инициативы, и более не требует обучения по этим стандартам, чего же вы не вернули в школы условного Киселёва?” Да, вернуть Киселёва в школы, безусловно, нужно, и я как могу, пытаюсь на это влиять. Но суть не в этом. Суть в том, что если на данный момент всё равно решает штат — на кой тогда мне нужен федеральный чиновник? Чего он в моей жизни меняет, кроме как сосания моих налоговых денег? Ничего он не меняет, и от его ухода хуже точно не станет.

Чего у нас там ещё осталось из функций Минобразования? А, внедрение “равенства” в образовании. Тут надо отметить, что используется английское слово equity, а не equality — то-есть, равенство результатов, а не равенство возможностей. Что в итоге означает то, что дурак и умный будут знать одинаково — то-есть, оба будут обучены отвратительно. Уже много раз видели. Как только начинаются разговоры о том, как насильно всех сделать равными — жди беды.

Чего ещё? Ах, ну да, гранты и финансовая поддержка. Но поддержка КОГО?

Вот пойдём на сайт Минобразования и поглядим на пару примеров, кому и на что они дают гранты.

https://www.ed.gov/grants-and-programs/apply-grant/available-grants:

“Программа Центра образовательного совершенства для чернокожих учителей в колледжах и университетах с историческим черным населением (CEEBT) предназначена для поддержки образцового центра образовательного совершенства в одном или нескольких высших учебных заведениях с высоким уровнем образования (HBCU), которые продемонстрировали доказанную репутацию в области выпуска высококвалифицированных, хорошо подготовленных чернокожих учителей.”

“Программа D2 предоставляет гранты государственным образовательным агентствам (SEA) в консорциумах с местными образовательными агентствами (LEA) для получения и оценки дезагрегированных данных по субпопуляциям AAPI для изучающих английский язык (EL) за пределами существующих семи расовых и этнических категорий в школьном сообществе. Десегрегированные данные будут использоваться для определения целевых стратегий по закрытию пробелов в образовательных возможностях.”

“Эта программа предоставляет дискреционные гранты общественным организациям, в первую очередь обслуживающим и представляющим коренных гавайцев, для планирования, проведения и администрирования программ карьеры и технического образования (CTE), которые ведут к получению годичных сертификатов или двухлетних степеней.”

“Цель программы — помочь американским индейцам с ограниченными возможностями, в соответствии с сильными сторонами, ресурсами, приоритетами, проблемами, способностями, возможностями, интересами и осознанным выбором таких людей, чтобы такие люди могли подготовиться и заняться высококачественной работой, которая увеличит возможности для экономической самодостаточности. Услуги программы предоставляются в соответствии с индивидуальным планом трудоустройства и могут включать услуги традиционного лечения.”

На коренных гавайцев и индейских шаманов-инвалидов у нас, получается, деньги есть. А на нормальную школьную программу по математике — извините, нет. И это ещё 2025 год, многое из доступных грантов оттуда поубирали. А в 2024 году там ещё деньги детям нелегальных мигрантов давали, чтобы в институт пойти учиться. Поглядите на archive.org если интересно.

Нам точно нужно это федеральное ведомство? Не отрицая никак проблемы образования отдельных меньшинств, я глубоко убеждён, что на федеральном уровне их не решить, никак. Такие вещи вообще надо решать максимум на уровне города, даже не на уровне штата. И уж совершенно точно — не на уровне засевших на речке Потомак государственных чиновников, большинство из которых даже учителями никогда не работали.

По-моему, правильно их собираются разогнать. Поддерживаю.

В Ноябре сего года у меня намечается совсем маленькая, на три дня, поездка в Турцию. Немного учу турецкий язык: как показывает опыт, если местные видят, что ты честно пытаешься говорить на их языке, отношение сразу сильно меняется в положительную сторону.

Турецкий язык, конечно, сильно не похож на языки, с которыми я ранее был знаком. Умляуты я, конечно, раньше видел, когда учил немецкий. А вот с седильями (Ç, Ş) сталкиваюсь впервые. Бреве, сиречь кратку, я, конечно же, уже использовал — в русском Й, но бреве над согласными, помимо чешской Č, раньше не наблюдал. Ну, и наличие как ı, без точки, и i сильно прикалывает. Некоторые слова забодаесся читать со всеми этими прибамбасами, хотя в целом норм, это вам не слова-паззлы в английском, типа “Leicester” (читается как “Лестер”).

Я уж не говорю про ирландский!! Например, распространённое ирландское женское имя Siobhan это никакая не “Сиобхан”, а вообще “Шивон”. А Saoirse — это “Сирша”. Ага, знай наших.

Но! Удивило меня всё же не это, а какое количество тюркизмов существует в русском языке. И некоторые турецкие слова отсюда понятны интуитивно — через русский. Сразу видно, как долго культуры контактировали и друг друга перекрёстно опыляли, натурально заклятые друзья, frenemies

Вот в русском языке есть слово “главный” или “глава”, например, “глава городской администрации” — высшее должностное лицо. Отсюда же — “главарь”. Оно понятно, почему вот так — начальник есть голова всей организации, без головы никуда. В английском тоже в том же смысле используется слово “голова”, например, “headmaster” это директор школы.

Так вот “начальник”, “главный”, “министр”, “управляющий” и подобное в турецком языке называется сразу же интуитивно понятным словом: БАШКАН (BAŞKAN). И всё незамедлительно кристально ясно.

В посте будет мат, ибо выбесили.

Пиратство — это нехорошо, и люди должны быть вознаграждены за свой труд. Книги я покупаю довольно часто, в основном электронные. Иногда, чтобы понять, стоит ли покупать книгу, я знакомлюсь с ней сначала через пиратский сайт https://libgen.is/. Если стоит, то без всяких проблем её покупаю.

А недавно я узнал, что копирасты пытаются засудить этот сайт. Если бы это сделали отдельные авторы — я бы понял, и отнёсся с сочувствием. Но это сделали не авторы, а издатели, в основном учебников. А учебники в США — это, блядь, не просто так книги. Это самый настоящий рэкет.

Среди моих читателей, наверное, немного людей, получивших бакалавра или выше в США, поэтому опишу навскидку, какая — в отдельных моментах — это ересь.

Вот, например, учебник, по которому меня учили в универе матану. Обратите внимание на его стоимость, блин!

Вот с какого хуя учебник по матану, который не менялся, поди, аж с Готтфрида Лейбница, стоит под триста монет, а? Меня учили по первому изданию этой книги, а не по девятому, так вот можно башку наотруб давать, принципиально внутри неё — ничего не изменилось. А? Чо? Купить бэушную книгу? А вот хуй тебе. Потому что внутри книги ещё есть уникальный код доступа к онлайн-сайту козлоиздателей, где ты будешь делать свою домашнюю работу. Домашнюю работу твою будет проверять вебсайт, а не преподаватель. Преподаватель он так… можно сказать, практически, для мебели.

Иногда (иногда) можно было купить бэушную книгу, и отдельно купить код доступа к сайту с домашней работой. Можно было таким образом сэкономить полтинник. Это сейчас мне полтинник в семестр это фигня. А когда я работал и учился, и платил за обучение сам, даже такие суммы были чувствительными. Зато кредитов выше крыши не набрал, закончил без долгов.

Так что теперь, когда все эти Сенгейджи, Пирсоны, и прочие Макгро Хиллы плачутся в сомбреро в стиле “да, мы охуели”, мой ответ — ИДИТЕ В ХУЙ. В жопу себе свои книжки запихните плашмя и проверните пару раз. Это в том числе и такие пидоры, как вы, создали эту систему, благодаря которой университетское обучение в США, пусть даже лучшее в мире, стоит так дорого.

В комментах к прошлому посту выяснилось, что не все знают, как СССР испортил преподавание математики в школах в 1970-1978 годах.

Самые худшие злодеяния совершаются, как известно, из самых лучших побуждений.

Группа инициативных советских математиков под руководством Колмогорова решила изменить как преподаётся математика в средних школах. Мол, мы живём во время науки и техники, а детей учим по дореволюционному учебнику Киселёва (что было сущей правдой — и мою бабушку, и моего отца учили именно по Киселёву).

Основная претензия маститых академиков к Киселёву состояла в том, что в его учебниках есть “неточности”, “допущения”, и что учебник “не является строго математически точным”. Что формально тоже правда. НО! Почему там были “неточности” и “допущения”? Что, кандидат наук Киселёв не знал математику? Разумеется, знал! Но главное отличие Киселёва от маститых академиков было в том, что в отличие от них, Андрей Петрович 20 с лихером лет преподавал математику в гимназиях и училищах. И именно потому, что он был Учителем, он знал, как именно нужно давать математику детям разных возрастов. Ведь ум ребёнка постоянно развивается — и вместе с ним его способности к пространственному воображению, абстрактному мышлению, и так далее. Если мы начнём фигачить в пятиклассника преподаванием на уровне университета, он ничему не научится.

Но академики пробили свою инициативу и решили, что им лучше видно, и начали писать свои учебники и портить киселёвские (особенно отличился на этом поприще некий Глаголев). В результате в учебниках математики и геометрии для средней советской школы появились абсолютно точные математически определения, доказательства и теоремы… абсолютно непонятные школьнику, ибо заумь.

Не буду голословным.

Все знают, что такое равные треугольники?

Вот доказательства того, что треугольники равны, если у них две одинаковые стороны, и одинаков угол между ними. Сначала — учебник 1980х Погорелова (по которому учили меня), а потом — Киселёв.

Ну чо, всё поняли? Я до сих пор нихера не понимаю. Луч, полуплоскость какая-то, и что меня добивает — иллюстрация якобы равных треугольников, явно не совпадающих друг с другом.

А теперь — умница наш Андрей Петрович Киселёв:

Вот тут всё предельно понятно, не так ли? Треугольники наложились и совпали? Конечно. И всё сразу ясно.

Но академики взъелись — чо тут? Какая это “точка”? Её правильно называть “вершиной!” И так далее и пошло-поехало. А то, что теперь эту заумь даже взрослый мужик не понимает — ну, не наши проблемы. В наших доказательствах и теоремах зато всё точно!!

И каков же был результат? Результат был АХОВЫЙ. В 1980х годах, казалось бы, в “золотые годы” советского образования стандартные задачки из дореволюционного задачника по математике решало вдвое меньше учеников. Я уж не говорю о гимназических контрольных — их вообще могли решать только школьники математических спецшкол.

Пример задачки для пятого класса: В классе 28 человек. Отношение числа девочек к числу мальчиков равно 4/3. Сколько в классе девочек?

В 1950м году её решило 83% пятиклассников. В 1995 — 37%!! То-есть, это вообще регресс, причём регресс абсолютный!

Спасибо вам, маститые академики, вы добились чего хотели — стало хуже. А советские школьные учебники теперь я вспоминаю исключительно матом.

Я бы хотел тут добавить “а зато в Америке….” но, увы, не могу. Американское школьное преподавание математики разломали ещё в 1960х (из тех же благих побуждений, ёпрст — они решили, что математику надо преподавать “лучше”, так как СССР обгонял США в космической гонке). А недавние инициативы “No Child Left Behind” и “Common Core” опустили планку обучения вообще ниже плинтуса. У меня и свояченица и тёща учители. О новомодных введениях, которые запустили ещё при Буше-младшем они говорят исключительно нецензурными словами.

Одна из вещей в США, о которой у меня очень неприглядное впечатление — это американское среднее образование. Если не жить в местах типа Массачуссетса или Коннектикута, то образование будет на уровне бедных стран Латинской Америки.

Высшее образование — прекрасное. А вот среднее… Я не знаю, как сейчас, а когда я учился, то русское среднее образование было заметно лучше американского, даже несмотря на идиотскую школьную реформу 1970х. Я, безусловно, ходил не в очень простую школу, но ёлки-палки…

Особенно ярко это видно на некоторых примерах по преподаванию математики. Чтобы преподавать математику в американской школе, даже не надо иметь высшее математическое образование. Более того, часто случается так, что преподают не учитель, а заместитель (substitute). Он мало того, что не обязан иметь математическое образование — он может вообще не уметь ни читать ни считать. К нему вообще никаких требований — он заместитель. Бывает так, что заместитель может учить детей целый год. Например, учитель математики пенсионного возраста получил травму и решил выйти на пенсию — пока не найдут нового, учить будет заместитель. У моей дражайшей супруги математику так учил физрук целый год. Вся математика из этого периода для неё — некая чёрная дыра. Она не умеет самых элементарных вещей — например, построить график функции.

Вы можете себе представить выпускника советской школы (не двоечника, а минимум хорошиста), который не может построить график y = 2x, например? И я не могу.

И это мы ещё живём в городе, где одни из лучших школ в штате. Что творится в (гре)бенях — и представить жутко.

А теперь — слайды! Для нешпрехающих кратко перевожу.

Марти съел 4/6 своей пиццы, а Луис 5/6. Марти съел больше пиццы. Как такое возможно?

Ответ (совершенно правильный) — у Марти пицца была большего размера.
Ответ учителя — а вот нихера это не возможно, так как 5/6 больше 4/6.

Используя метод сложения, рассчитайте значение 5 * 3.

Ответ: 5 + 5 + 5 = 15
Ответ учителя: а вот неверно: 3 + 3 + 3 + 3 + 3! Перемена мест сомножителей? Нет, не слышали.

И наконец, вишенка на торте.

“Не пиши курсивом, ты в первом классе! Подожди до третьего класса”. Не выё…пендривайтесь, слушайте свои “Валенки”, ага.

Напляшемся мы ещё с этими школами.

Профессора Калифорнийского Университета (Лос Анжелес) признали виновным в передаче военных микросхем китайцам. Согласно обвинительному заключению, профессор Йи-Чи Ши незаконно приобрёл военные микросхемы производства неназванной компании. Заполучив микросхемы, профессор переправил их в Китай. Теперь профессору светит нехилый срок до 219 лет.

Мои личные впечатления от учёбы в американских ВУЗах целиком подтверждают возможность подобного. У нас идёт утечка мозгов наоборот — китайцы постоянно приезжают сюда учиться. В университетах проводится огромная исследовательская работа по темам, которых ещё в учебниках нет. Китайские студенты тоже участвуют в этих исследованиях, а потом весь багаж полученных таким образом новейших знаний увозят назад в Китай. Постоянно такое видел. Своими собственными руками, получается, повышаем уровень потенциального противника.

Повспоминал всякое, посмеялся. Я когда только начинал учиться в американском универе, тоже решал всё “по-русски”. За преподами было забавно наблюдать — “Это как? Это откуда ты написал? Ааа….” Т.е. требовалась пара секунд понять, что у меня всё правильно, просто подход другой.

Самое большое офигение вызвала моя запись деления в столбик. Я же в своё время офигел от того, как лихо местные раскладывают квадратные уравнения на множители. Нас так делать, конечно, тоже учили, но как-то не делали это основным способом решения квадратных уравнений. А тут сначала всегда пробуют разложить на множители, а только потом уже, если не получается, вставлять в формулу.

Но больше всего я офигел от т.н. “algebraic long division“, деления многочлена на многочлен. Нас такому вообще не учили, а тут это является стандартной операцией.